As an undergraduate, I once took a course in mathematical modeling, which ended up having a huge influence on my academic interests. The course was very light on technological tools, with almost all work being done by hand. Early in the course, the professor posed a remarkable problem as a homework exercise. I became so fond of the problem that I later tracked down its original source and bought an old copy of the book:

The problem in question is stated as follows (first paragraph):

No matter how heavy the snowfall, a snowplow traveling two miles in an hour seems a bit unrealistic to me – at least in this century. So as an update, let’s make a slight change and try to solve the following problem instead:

Despite being drawn from a text on the lofty subject of differential equations, this problem should be solvable by anyone who has had college-level Calculus I, or a year of high school calculus. The hardest part of the problem is not the math required to solve it, but the fact that you must make some assumption on your own about the relationship between snow and plowing speed. That is, how does the speed of a snowplow depend on the depth of the snow on the ground? The simplest reasonable assumption is this: The speed of a snowplow is inversely proportional to the depth of the snow it is plowing at each moment. Though it may be hard to believe, this assumption and the information given in the problem are enough to calculate a definite solution.
Back in college, I solved the homework problem for my mathematical modeling course by hand on paper using a little calculus, but I have often wondered how a student might approach the problem if they didn’t know any calculus, but did have some ability to program. Many (if not all) “calculus problems” can be solved through fairly simple computer programming, and it turns out that this one is no exception.
First approach
As is so often the case, I’ll do my work here in Python. We’ll simulate a snowplow making its way through a steady snowfall. First, let’s set the starting amount of snow (in inches):
snow_depth = 1
Let’s set how long it has been snowing (in units of time):
head_start = 1000
These two numbers are complete guesses; they can be varied, and the subsequent code run again, to see if the final conclusion changes. With a starting snow depth of 1 inch and a “head start” of 1000 units of time, we are implicitly saying that it’s snowing at a rate of 0.001 inches per unit of time.
snow_rate = snow_depth / head_start
If the unit of time is one second, this would be a fairly heavy (but not unreasonable) rate of snowfall.
We’re going to keep track of the distance traveled at each moment as a list (starting with distance 0 miles at the beginning):
dist = [0]
Now we’ll run the simulation, increasing the snow on the ground and moving the snowplow until the distance traveled in the second half of the simulation falls below half the distance from the first half of the simulation:
while (
len(dist) % 2 == 0
or dist[-1] - dist[len(dist)//2] >= dist[len(dist)//2] / 2
):
# Snow a bit
snow_depth += snow_rate
# Adjust the plow speed
speed = .01 / snow_depth
# Move forward a bit
dist.append(dist[-1] + speed)
The constant in the speed line (0.01) should of course be varied to see if it affects the conclusion. If the unit of time is one second, the value 0.01 I’ve chosen arbitrarily here would mean that the snowplow travels at 36 mph when there’s 1 inch of snow on the ground, which probably isn’t too unreasonable.
Of course, there’s no reason to suppose the unit of time is one second; in fact, if we determine what the unit of time really is, then the answer to the problem is simply 1000 times that unit. When we run the “while” loop above, it will terminate after a certain number of units of time, which are supposed to correspond to 2 hours. This allows us to calculate the answer:
print('There are %d units of time in two hours,' % (len(dist) - 1))
ans = 2 / (len(dist) - 1) * head_start
print('so it started snowing %.3f hours before noon.' % ans)
The reported answer is: “There are 3238 units of time in two hours, so it started snowing 0.618 hours before noon.” If we vary the “snow depth,” “head start” (within reason), and speed constant, they do not have any noticeable effect on this final result.
Second approach
I think a more rigorous approach would be something similar to the one I took in a certain trigonometry problem I wrote about before.
We’ll create a function that can take a “guess” about how many hours before noon it started snowing, and returns a measurement of the “error” – that is, how far the results are from the distance ratio required in the problem. Here is my function:
def plow_error(
time_before_noon, # hours before noon it started snowing
snow_rate, # inches per hour
time_step, # time (in hours) between simulation updates
speed_constant # speed (mph) of snowplow in 1 inch of snow
):
# Set the starting snow depth, time, and distance plowed
snow_depth = time_before_noon[-1] * snow_rate
current_time, distance = 0, 0
# This variable will store the distance after 1 hour
first_distance = None
# Go until 2 hours have passed
while current_time < 2:
# Update the time, snow some more, adjust the plow speed
current_time += time_step
snow_depth += snow_rate * time_step
speed = speed_constant / snow_depth
# Move the plow forward
distance += speed * time_step
# Store the distance at 1 hour
if first_distance is None and current_time >= 1:
first_distance = distance
# Report the squared error in distance ratio
return (distance / first_distance - 1.5) ** 2
So now to solve the problem, we can run the following:
from scipy.optimize import minimize
ans = minimize(plow_error, 0, args = (2, 1/3600, 15)).x[0]
print('It started snowing %.3f hours before noon.' % ans)
Again the reported answer is: “It started snowing 0.618 hours before noon.” The three parameters (or “args”) used above can be varied, with no real effect on the outcome. The values I chose here correspond to a snowfall rate of 2 inches per hour (fairly heavy), unit of time 1 second, and a snowplow that can travel 15 mph in 1 inch of snow. Also, I’m using an initial guess of 0 hours (i.e. it started snowing at noon).
A more thorough approach
You may have noticed that the two approaches above are a little careless in how they satisfy the condition demanded by the problem; they require that the snowplow should travel half the distance in the second hour that it traveled in the first, but they do not require the distances to be 20 miles and 10 miles specifically. One way to resolve this is as follows:
def plow_error(
inputvals,
snow_rate, # inches per hour
time_step # time (in hours) between simulation updates
):
time_before_noon, speed_constant = inputvals
# Set the starting snow depth, time, and distance plowed
snow_depth = time_before_noon * snow_rate
current_time, distance = 0, 0
# This variable will store the distance after 1 hour
first_distance = None
# Go until 2 hours have passed
while current_time < 2:
# Update the time, snow some more, adjust the plow speed
current_time += time_step
snow_depth += snow_rate * time_step
speed = speed_constant / snow_depth
# Move the plow forward
distance += speed * time_step
# Store the distance at 1 hour
if first_distance is None and current_time >= 1:
first_distance = distance
# Report the sum of squared error in the distances
return (first_distance - 20) ** 2 + (distance - 30) ** 2
There are only two real changes from before:
- The “speed constant” will now be subjected to the optimization process.
- The error returned is based on the actual distances required, not just their ratio.
To solve the problem:
from scipy.optimize import minimize
ans = minimize(plow_error, [0, 15], args = (2, 1/3600)).x
print(
'It started snowing %.3f hours before noon, '
'and the speed constant is %.0f inch-miles per hour.'
% tuple(ans)
)
The result: “It started snowing 0.618 hours before noon, and the speed constant is 42 inch-miles per hour.” Note that changing the snowfall rate will change the required speediness of the snowplow, but it still will not affect the answer to the original problem.
NetLogo simulation
NetLogo is an interesting programming environment that can be quite useful for creating agent-based models of processes with both a time and a spatial component. I became interested in ABM’s and NetLogo during my graduate school research in mathematical biology/ecology, though I never developed anything close to expertise in the NetLogo language.
Some time ago, I wrote an interactive simulation of the snowplow problem, with multiple snowplows and a somewhat increased level of realism. You can find the simulation at this link, where it can even be run inside your browser (see the “Run in NetLogo Web” tab). The simulation places some number of snowplows onto a two-dimensional field with some starting amount of snow, which increases at some steady rate. The plows move at a speed inversely proportional to the amount of snow under them, and they sometimes turn randomly when they reach a street intersection. The simulation keeps track of the average total distance traveled by the snowplows. Here’s a snapshot of the simulation running, with 5 snowplows in action:

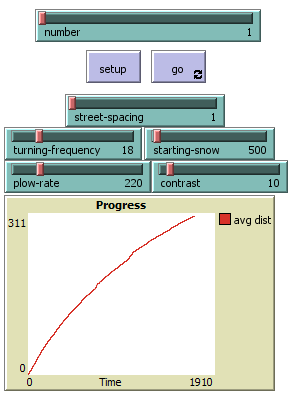
We can use this simulation to try to solve the problem from before, if we set the number of snowplows to 1. We should also lower the “street spacing” and “turning frequency” parameters, to decrease the chances of the snowplow running over its own path. I’ll set the “starting snow” to 500, which is the same as saying that it was snowing for 500 units of time before the snowplow started.
If we run the simulation as described above, it consistently takes about 1700 units of time to reach the distance ratio required in the problem, with the distance traveled in the second half of the simulation being half the distance traveled in the first half of the simulation. If 1700 units of time is 2 hours, then it was snowing for about 0.59 hours before the snowplow started, which is not too far off from our previous solutions!
Closing: the mathematical solution
Presh Talwalkar of Mind Your Decisions has made a great and thorough video explaining the purely mathematical approach to the snowplow problem. Note that the final solution is in close agreement with our first three approaches.